Research
I consider myself an engineer and scientist within the area of computational mechanics and applied mathematics. My research is in the intersection engineering, mathematics, physics, and computational science. In particular, I develop finite element methods for challenging problems in engineering science and physics.
My past research has resulted in the development of a new finite element method, called the Automatic Variationally Stable Finite Element (AVS-FE) method. Currently, much of my research efforts are focused on development of finite element methods and coupling of finite element methods to exploit the properties of individual methods and models across the coastal floodplain. A second ongoing research topic I devote a significant amount of effort to is the verification of new finite element meshes for the ADCIRC model to be used on the operational forecasting of hurricane storm surge on the US Gulf coast. I am also fortunate to work on a wide array of other smaller and larger projects with talented postdocs and Ph.D. students in the Computational Hydraulics group at the Oden Institute.
A significant portion of my work and research requires programming and development of computer codes. These codes are nearly always openly available online, see for example the ADCIRC website and my code repository of stable finite element methods implemented in FEniCS.
Finite Element Methods
My Ph.D. research, supervised by Albert Romkes, was spent focusing on the development of the AVS-FE method. This method is a discontinuous Petrov-Galerkin (DPG) method (developed by Leszek Demkowicz and Jay Gopalakrishnan) making the particular choice of fully continuous trial spaces. As the method is still in its early days of development, the focus has been verification of its properties for a wide range of engineering problems including convection-dominated diffusion, nearly incompressible elastostatics, Cahn-Hilliard equation, and wave propogation to mention a few. After starting my postdoctoral research, I have focused on analysis of the method as well as its application to the modeling of hurricane storm surge. Additionally, as part of a multi-institution ongoing National Science Foundation sponsored project, my work has also included further development of the existing finite element software named discontinuous Galerkin Shallow Water Equations model (DG-SWEM) for the use in complound flood modeling.
The AVS-FE Method
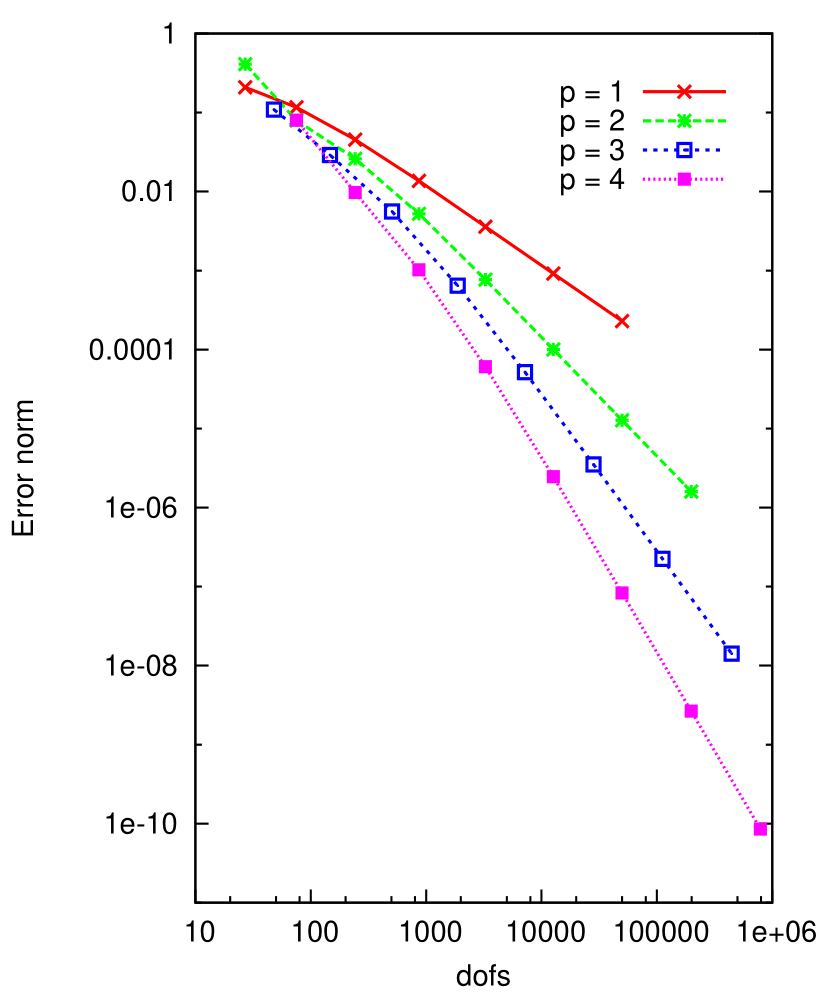
The AVS-FE method is uncondtionally stable, regardless of the underlying differential operator and FE mesh. The stability is derived from the DPG concept of optimal discontinuous test functions computed on-the-fly, whereas the trial space consist of classical FE basis functions.
Calo, V.M., Romkes, A., Valseth, E. (2020) Variationally Stable Analysis for Finite Element Computations: An Introduction Lecture Notes in Computational Science and Engineering [doi]
Goal-Orietned Error Estimation

The stability property of the AVS-FE allows us to establish approximations of the dual problem to the convection-domainated diffusion PDE which is necessary in goal-oriented error estimation. To ensure a continuous dual solution, we introduce a new approach in which we consider the dual PDE and its AVS-FE approximation. This leads to highly accurate error estimates even for convection dominated scenarios in which classical FE methods suffer from loss of stability. The first-order system description in the AVS-FE method also allows straightforward error estimation of fluxes.
Valseth, E. and Romkes, A., (2020) Goal-Oriented Error Estimation for the Automatic Variationally Stable FE Method for Convection-Dominated Diffusion Problems Computers and Mathematics with Applications [doi]
Applications
Mineral Separation

The extraction and refinement of minerals is generally requires vast amounts of water, in some cases up to 60,000 m3 per day. In an effort to reduce this amount of water a team of researchers at South Dakota School of Mines and Technology is working on novel refinement techniques under a NSF grant titeled Sustainable System for Mineral Beneficiation . As a mathematical model for the mineral separation, we use the Cahn-Hilliard equation and develop corresponding space-time finite element approximations in an effort to predict the mineral separation process. Working with metallurgists and mineral separation experts, a space-time AVS-FE method will be used to predict the mineral separation process and guide the design process of a new mineral separator.
Valseth, E., Romkes, A., and Kaul, A., (2020) A Stable FE Method For the Space-Time Solution of the Cahn-Hilliard Equation Journal of Computational Physics [doi]
Water Wave Propagation

In an ongoing sequence of papers, Clint Dawson and I are developing DPG methods for the mathematical modeling of hurricane storm surge. As an initial verification, we considered the Korteweg-de Vries equation, one of the simplest water wave mathematical models. Currently, we are working on more complex mathematical models such as the shallow water equations.
Valseth, E., Dawson, C. (2020) An Unconditionally Stable Space-Time FE Method for the Korteweg-de Vries Equation. Computer Methods in Applied Mechanics and Engineering 371:113297, [doi]
Shallow Water Flow

In the second paper in this sequence, we considered the 2D shallow water equations. We establish a priori error estimates as well a multiple numerical experiments to verify converegence behavior of our space-time FE approximations. We perform multiple verifiactions of physical benchmarks such as dam break and tidal fluctuations. Additionally, we confirm the well-balanced property of the method for the important lake-at-rest case.
Valseth, E., Dawson, C., (2020) A Stable Space-Time FE Method for the Shallow Water Equations Computational Geosciences [preprint]
Nearly Incompressible Materials

For modern enginerering materials such as polymers and composite materials, classical finite element methods often suffer from a loss of stability when the Poisson's ratio approach the incompressible limit. To present a robust method that does not loose stability in this limit, we introduce a weighted least squares FE method for nearly incompressible linear elastostatics. We establish a priori error bounds and several numerical verifications comparing our method to the classical Bubnov-Galerkiun and least squares FE methods. Numerical verifications exploiting a built-in error indicator in adaptive mesh refinements and consideration of a classical engineering structure, a beam, show the applicability of the method to challenging engineering applications.
Valseth, E., Romkes, R., Kaul, A., Dawson, C., (2021) A Stable Mixed FE Method for Nearly Incompressible Linear Elastostatics International Journal for Numerical Methods in Engineering [doi]
Coastal Modeling
In a sequence of projects and papers, we model and investiate the impacts of dredging a ship channel on the Texas Coast. We first consider the effects on estuarine dependent fish larvae through modeling coastal circulation and Lagrangian particle transport. In the second case, we consider the effects on hurricane storm surge magnitude and inundation. In particular, we study the impacts of Hurricane Harvey and synthesized versions of Harvey.
Modeling of Fish Larvae Transport
The Port of Corpus Christi is a busy shipping hub for shipping goods and materials to and from the United States. To reach the port, ships must travel through the 47 ft. deep man made ship channel which extends from the Aransas Pass to the port. To accomodate larger ships, an increase in the depth of this ship channel has been proposed. In collaboration with Ed Buskey of The Univeristy of Texas at Austin Marine Science Institute, we develop mathematical models governing the transport of Red drum fish larvae, modeled as passive Lagrangian particles. Our numerical models indicate negligible impacts of the proposed deeper channel on the transport of Red drum larvae from offshore breeding grounds through Aransas Pass to appropriate nursing grounds.
Valseth, E., Loveland, M., Dawson, C., Buskey, E., (2021) A Study of the Potential Impact of Dredging the Corpus Christi Ship Channel on Passive Particle Transport. Journal of Marine Science and Engineering [doi]
Modeling of Storm Surge
The Port of Corpus Christi is a busy shipping hub for shipping goods and materials to and from the United States. To reach the port, ships must travel through the 47 ft. deep man made ship channel which extends from the Aransas Pass to the port. To accomodate larger ships, an increase in the depth of this ship channel has been proposed. In collaboration with Ed Buskey of The Univeristy of Texas at Austin Marine Science Institute, we develop mathematical models governing hurricane storm surge. We apply the National Hurricane Center best track model and a Generalized Asymmetric Holland Model for hurricane wind and pressure fields. For the condisdered Hurricane Harvey and synthesized versions of Harvey, our model finds that most of the area near Corpus Christi will experience a reduced maximum surge magnitude, whereas some localized areas will see increased suge up to 15cm.
Valseth, E., Dawson, C., Buskey, E., (2023) A Study of the Potential Effects of Deepening the Corpus Christi Ship Channel on Hurricane Storm Surge. Journal of Computational Science
Accurate, efficient numerical models for storm surge are critical for both long-term risk assesment and to guide emergency management decisions during and before events. While high-fidelity hydrodynamic models such as the ADvanced CIRCulation (ADCIRC) model can accurately predict storm surge, they are very computationally expensive. In this paper, we develop a novel surrogate for the prediction of peak storm surge based on a multi-stage approach. In the first stage, points are classified as inundated or not. In the second, the level of inundation is predicted for each point. Within the new fromulation, we propose a surrogate in which storm surge is predicted independently for each point. This allows for predictions to be made directly for locations not present in the training data, and leads to a reductuib in the number of required model parameters. We our framework on two vastly diffrent study areas: the Texas coast and the northern portion of the Alaskan coast. For Texas, the model is trained with a large database of synthetic hurricanes, whereas for Alaska, the model is trained on a dataset of 109 historical surge events. We test the surrogate model on actual surge events including the recent Typhoon Merbok (2022) in Alsaska and Hurricane Harvey (2017) in Texas that take place after the events in the training data.
Pachev, B., Arora, P., del-Castillo-Negrete, C., Valseth, E., & Dawson, C., (2023) A framework for flexible peak storm surge prediction. Coastal engineering [doi]
Disease and Flood Modeling
A recent report by the World Health Organization, noted the effects of the changing climate on the spread of infectious diseases. For example, after flooding events, increased transmission of diseases such as Malaria has been frequently noted and observed. In a project recently funded by the Wellcome Trust, we investigate and seek to develop new integrated flood and disease models to better predict and understand the interplay between the two processes.
